https://arxiv.org/abs/2305.13404
Introduction
DNNでは、局所最適解の存在により、同じ損失をとっても異なるパラメタをとるときがよくある。しかし、地点により勾配が違うので、どうせ降下するし、パラメタが十分に多いなら局所最適解でも十分に良いなら、同じような損失関数の値をとるが勾配がより急な点に移って、そこで勾配降下法を解けば素早く収束しないか?=Teleportation。
しかし、それの理論的なnot convex関数での収束の保証はまだ存在してない。
今までは学習の加速のみ考えられていたが、仮定のもとでTelepotationではモデルの汎化性能まで上がるとも分かった。
そして、SGDのみならずAdaGrad、RMSProp、Adamにも適用した。
Related Works
パラメタ空間の対称性
対称性があるということは、DNNが特定の変換を施しても損失関数が変わらない性質をいう。
例)すべてのパラメタを等倍しても出力は変わらない、重み行列の列ベクトルを入れ替える、今の層でスケーリングしても次の層で縮めるとか。
対称性を持つと、明確に異なるパラメタであっても同じ損失を持つ点を持つ。
最小値のsharpnessと汎化性能
より周辺のgradientが平坦な局所最適解は一般的にrobustである。
鋭さは以下のような測り方がある。
- ヘッセ行列の小さな(なだらかな方向)の固有値の数が多いほど緩い。
- ヘッセ行列は対称行列で、それを対角化することは各軸ごとの曲率(高いほど急に曲がっている)を得ることができる。
- ヘッセ行列の大きい順に個の固有値の積をとる。
- 最小値の点の近傍にある最大の損失をとる値。
なぜTeleportationは有効なのか
なぜTeleportationは周囲が平たんな最小値に収束するのかをニュートン法をベースで証明した。これは1次や2次収束の間の速度。
対称Teleportationとは何か
パラメタ空間に作用する群に属するすべての元について、パラメタの変換を定義して、で変換しても、損失が変わらないが保証されないといけない。その中で、Gradientのを最大化するものを選んで、そこに手レポートする。それを対称Teleportationという。
具体的な実現は、今の層で倍して、次の層で倍する、行列の列ベクトルを入れ替えるなど。
群とは、加法について閉じていて、結合法則、単位元、逆元が存在するというもの。
この時、勾配降下法では、からGradientを計算して更新するのではなく、以下のようにテレポートしてそこでの勾配を利用して更新する。
定理3.1: Teleportationしても勾配のノルムは学習が進むにつれて小さくなるしどんどん上限を持つ。
内容
- 学習によって得られたモデルのパラメタ、ミニバッチを考える。
- 。学習で得られたモデルのパラメタを使うのと、今のミニバッチに最適なパラメタを使う。
- 最大なGradientについて、変換のを考える。
- ステップサイズをとする。
この時、以下のように有界であり、とすれば確かに収束する。
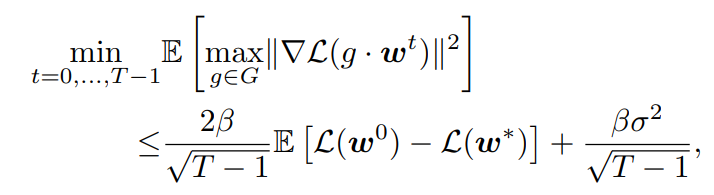
証明は、β-smootheならば、以下の式がSGDで成り立つ。
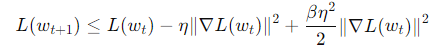
Teleportationしても、問題ないらしい。学習率を反復回数に従い減っていくスケジューラーに従うとすれば、おのずと得ることができる。
ニュートン法とTeleportation
定理3.2: Teleporation付きのSGDは、ニュートン法と同じ二次収束であるから確かに早い。
内容
- 勾配を最大化するようなを選ぶ。
- をヘッセ行列だとして、その中の最大の固有値をとする。
- Gradient Descendは以下のように行われる。
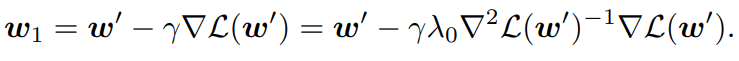
- 収束保証が以下のように、二次収束となる。
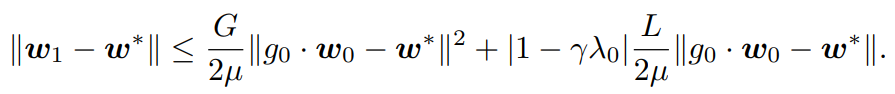
毎回できるだけ最急のGradientを選べるので、数が増えればどんどんニュートン法のように迅速な勾配降下になる。
Teleportationのタイミング
常にTeleporationするのは計算コストが高い。実は1回だけすればいいということがある。
これは以下の条件が必要。満たせば1回すれば、ニュートン法並みの効果が得られる。
- 勾配の方向と最適化の経路が一致している。
- Teleportation後の曲率について、μ強凸性(ヘッセ行列の最小固有値がμ以上)、L-スムーズ性(指定区間の?リプシッツ定数がL以下?)を満たす。
Teleportationによる汎化性能の向上
最小値の鋭さの定義
いろんな鋭さの定義があるが、以下のように半径の単位球からランダムに伸ばしたベクトルについて、損失の変動の平均をとる。
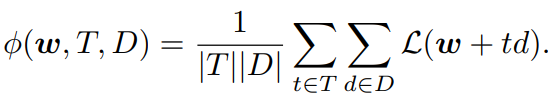
最小値の曲率
ヘッセ行列の固有値が0、である固有ベクトルは、その向きに動かすことでほぼ値は変化しない。
通常はヘッセ行列の固有値で評価する。高ければその固有ベクトルの向きに大きく変化していることを意味している。
上位k個とか、最大固有値とかなど。
しかし、これでは平坦な方向(小さい固有値)の影響を正確に反映できないし、固有値0の鞍点の意味が分からない。そして、固有ベクトル間の相互関係を捉えていない。
ここで、新しい曲率の指標を提案する。
リー代数を使う。📄Lie代数まとめ
今回の論文では、DNNの層構造に対称性にリー群とリー代数を使う。層ごとの重み行列が変換されても損失関数が変わらないような対称性を持つ。
なんか、よくわからなかったです!
汎化性能との相関
まだよく研究されていない。
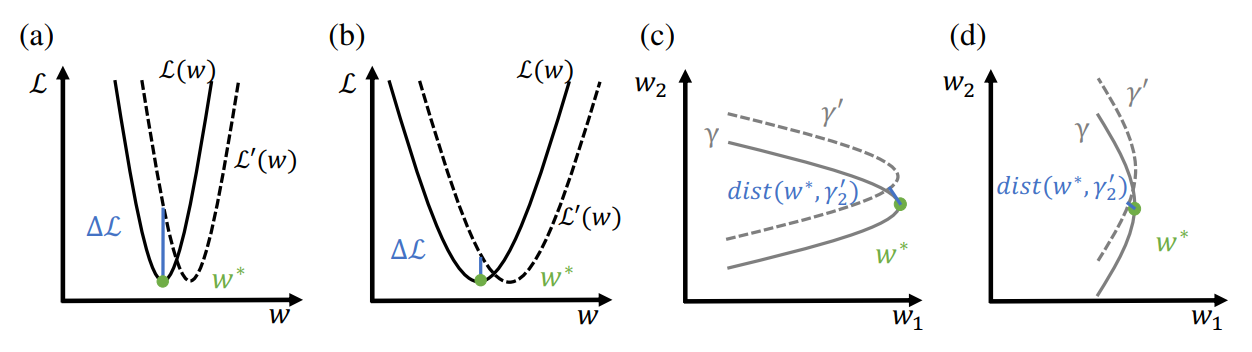
(a),(b)のように最小点での変化する量が大きいければ、鋭い。
平坦な点にTeleportationすると、汎化性能が少し改善されるが、鋭い点にTeleportationしても改善されない。
これは、学習の途中で行うwarm restartと同じような効果が見えているらしい。
最適化手法への応用
SGDの場合、
